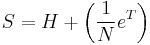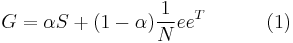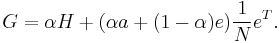Google matrix

A Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages. The rank of each page can be generated iteratively from the Google matrix using the power method. However, in order for the power method to converge, the matrix must be stochastic, irreducible and aperiodic.

1 H matrix
2 G matrix
3 Spectrum and eigenstates of G matrix
4 Historical notes
5 See also
6 References

H matrix

In order to generate the Google matrix, we must first generate a matrix H representing the relations between pages or nodes.

Assuming there are n pages, we can fill out H by doing the following:

Fill in each entry 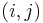$(i, j)$ with a 1 if node $i$ has a link to node $j$ , and 0 otherwise; this is the adjacency matrix of links.
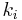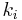Divide each row by $k_i$ where $k_i$ is the total number of links to other pages from node i. The matrix H is usually not stochastic, irreducible, or aperiodic, that makes it unsuitable for the PageRank algorithm.

G matrix

Given H, we can generate G by making H stochastic, irreducible, and aperiodic.

We can first generate the stochastic matrix S from H by adding an edge from every sink state $a$ to every other node. In the case where there is only one sink state the matrix S is written as:

$S=H%2B\left(\frac{1}{N}e^T\right)$

where N is the number of nodes.

Then, by creating a relation between nodes without a relation with a factor of $\alpha$ , the matrix will become irreducible. By making $H$ irreducible, we are also making it aperiodic.

The final Google matrix G can be computed as:

$G = \alpha S %2B (1-\alpha) \frac{1}{N} e e^T \;\;\;\;\;\;\;\;\;\;\; (1)$

By the construction the sum of all non-negative elements inside each matrix column is equal to unit. If combined with the H computed above and with the assumption of a single sink node $a$ , the Google matrix can be written as:

$G = \alpha H %2B (\alpha a %2B (1-\alpha)e) \frac{1}{N} e^T.$

Although G is a dense matrix, it is computable using H which is a sparse matrix. Usually for modern directed networks the matrix H has only about ten nonzero elements in a line, thus only about 10N multiplications are needed to multiply a vector by matrix G[1,2]. An example of the matrix $S$ construction for Eq.(1) within a simple network is given in the article CheiRank.

For the actual matrix, Google uses a damping factor $\alpha$ around 0.85 [1,2,3]. The term 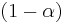$(1-\alpha)$ gives a surfer probability to jump randomly on any page. The matrix $G$ belongs to the class of Perron-Frobenius operators of Markov chains [1]. The examples of Google matrix structure are shown in Fig.1 for Wikipedia articles hyperlink network in 2009 at small scale and in Fig.2 for University of Cambridge network in 2006 at large scale.

Spectrum and eigenstates of G matrix

For 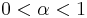$0 < \alpha < 1$ there is only one maximal eigenvalue 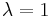$\lambda =1$ with the corresponding right eigenvector which has non-negative elements 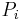$P_i$ which can be viewed as stationary probability distribution [1]. These probabilities ordered by their decreasing values give the PageRank vector 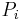$P_i$ with the RageRank 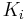$K_i$ used by Google search to rank webpages. 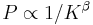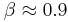Usually one has for the World Wide Web that $P \propto 1/K^{\beta}$ with $\beta \approx 0.9$ . The number of nodes with a given PageRank value scales as 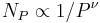$N_P \propto 1/P^\nu$ with the exponent 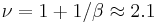$\nu = 1%2B1/\beta \approx 2.1$ [4,5]. The left eigenvector at 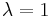$\lambda =1$ has constant matrix elements. With 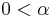$0 < \alpha$ all eigenvalues move as 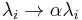$\lambda_i \rightarrow \alpha \lambda_i$ except the maximal eigenvalue 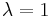$\lambda =1$ , which remains unchanged [1]. 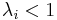The PageRank vector varies with $\alpha$ but other eigenvectors with $\lambda_i < 1$ remain unchanged due to their orthogonality to the constant left vector at 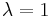$\lambda = 1$ . The gap between 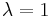$\lambda = 1$ and other eigenvalue is 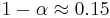$1 - \alpha \approx 0.15$ gives a rapid convergence of a random initial vector to the PageRank approximately after 50 multiplications on $G$ matrix.

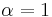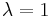At $\alpha=1$ the matrix $G$ has generally many degenerate eigenvalues $\lambda =1$ (see e.g. [6,7]). Examples of the eigenvalue spectrum of the Google matrix of various directed networks is shown in Fig.3 from [14] and Fig.4 from [7].

The Google matrix can be also constructed for the Ulam networks generated by the Ulam method [8] for dynamical maps. The spectral properties of such matrices are discussed in [9,10,11,12,13,14,15,16]. In a number of cases the spectrum is described by the fractal Weyl law [10,12].

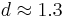The Google matrix can be constructed also for other directed networks, e.g. for the procedure call network of the Linux Kernel software introduced in [15]. In this case the spectrum of $\lambda$ is described by the fractal Weyl law with the fractal dimension $d \approx 1.3$ (see Fig.5 from [16]). Numerical analysis shows that the eigenstates of matrix $G$ are localized (see Fig.6 from [16]). Arnoldi iteration method allows to compute many eigenvalues and eigenvectors for matrices of rather large size [13,14,16].

Other examples of $G$ matrix include the Google matrix of brain [17] and business process management [18], see also [19].

Historical notes

The Google matrix with damping factor was described by Sergey Brin and Larry Page in 1998 [20], see also articles PageRank and [21],[22].

References

[1] Langville, Amity N; Carl Meyer (2006). Google's PageRank and Beyond. Princeton University Press. ISBN 0-691-12202-4.
[2] Austin, David (2008). "How Google Finds Your Needle in the Web's Haystack". AMS Feature Columns. http://www.ams.org/samplings/feature-column/fcarc-pagerank
[3] Law, Edith (2008). "PageRank" (PDF). http://scienceoftheweb.org/15-396/lectures/PageRank_Lecture12.pdf
[4] Donato D.; Laura L., Leonardi S., Millozzi S. (2004). "Large scale properties of the Webgraph". Eur. Phys. J. B v.38, p.239
[5] Pandurangan G.; Ranghavan P., Upfal E. (2005). "Using PageRank to Characterize Web Structure". Internet Math. v.3, p. 1
[6] Serra-Capizzano, Stefano (2005). "Jordan Canonical Form of the Google Matrix: a Potential Contribution to the PageRank Computatin". SIAM J. Matrix. Anal. Appl. v.27, p.305
[7] Georgeot B.; Giraud O., Shepelyansky D.L. (2010). "Spectral properties of the Google matrix of the World Wide Web and other directed networks". Phys. Rev. E v.81, p.056109
[8] Ulam, Stanislaw (1960). "A Collection of mathematical problems, Interscience tracs in pure and applied mathematics". Interscience, New York p.73
[9] Froyland G.; Padberg K. (2009). "Almost-invariant sets and invariant manifolds — Connecting probabilistic and geometric descriptions of coherent structures in flows". Physica D v.238, p.1507
[10] Shepelyansky D.L.; Zhirov O.V. (2010). "Google matrix, dynamical attractors and Ulam networks". Phys. Rev. E v.81, p.036213
[11] Ermann L.; Shepelyansky D.L. (2010). "Google matrix and Ulam networks of intermittency maps". Phys. Rev. E v.81, p.036221
[12] Ermann L.; Shepelyansky D.L. (2010). "Ulam method and fractal Weyl law for Perron-Frobenius operators". Eur. Phys. J. B v.75, p.299
[13] Frahm K.M.; Shepelyansky D.L. (2010). "Ulam method for the Chirikov standard map". Eur. Phys. J. B v.76, p.57
[14] Frahm K.M.; Georgeot B, Shepelyansky D.L. (2011). Universal emergence of PageRank. J. Phys. A: Mat. Theor. v.44, p.465101. arXiv:1105.1062
[15] Chepelianskii, Alexei D. (2010). Towards physical laws for software architecture. arXiv:1003.5455
[16] Ermann L.; Chepelianskii A.D., Shepelyansky D.L. (2011). "Fractal Weyl law for Linux Kernel Architecture". Eur. Phys. J. B v.79, p.115. arXiv:1005.1395
[17] Shepelyansky D.L.; Zhirov O.V. (2010). "Towards Google matrix of brain". Phys. Lett. A v.374, p.3206
[18] Abel M.; Shepelyansky D.L. (2011). "Google matrix of business process management". Eur. Phys. J. B v.84, p.493. arXiv:1009.2631
[19] Ermann L.; Chepelianskii A.D, Shepelyansky D.L. (2011). Towards two-dimensional search engines. arXiv:1106.6215
[20] Brin S.; Page L. (1998). "The anatomy of a large-scale hypertextual Web search engine". Computer Networks and ISDN Systems v.30, p.107
[21] Franceschet, Massimo (2010). PageRank: Standing on the shoulders of giants. arXiv:1002.2858
[22] Vigna, Sebastiano (2010). "Spectral Ranking". personal webpage. http://vigna.dsi.unimi.it/ftp/papers/SpectralRanking.pdf